| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
- 알고리즘
- 쉘
- 리눅스
- 프로세스
- c
- 백준알고리즘
- Windows10
- linux
- 백준
- 회귀
- Windows 10
- 텐서플로우
- 프로그래밍
- TensorFlow
- 학습
- 영상처리
- 턱걸이
- CV
- 시스템프로그래밍
- OpenCV
- 운영체제
- shell
- 딥러닝
- python
- Computer Vision
- C++
- 공부
- error
- 코딩
- C언어
- Today
- Total
줘이리의 인생적기
[tensorflow 10] 선형회귀01 본문
데이터의 경향성을 잘 설명하는 하나의 직선을 예측하는 선형 회귀(Linear Regression)에 대해 공부해보겠습니다.
예를 들어, 키와 몸무게 2개의 데이터 경향성을 보면 키가 클수록 몸무게가 많이 나갈 확률이 높습니다.
또, 날씨의 온도와 호빵의 판매량 2개의 데이터 경향성을 보면 날씨가 추울수록 호빵이 많이 판매될 확률이 높습니다.
저는 통계청에 재미있는 통계들이 많이 있어서 2개의 데이터를 뽑아 어떤 경향성이 있는지 확인해보려고 합니다.
kosis.kr/easyViewStatis/visualizationIndex.do
KOSIS 국가통계포털
kosis.kr
저는 이 곳에서 2017년 지역별로 학령인구와 고령인구비율 데이터를 가지고 이 두 데이터가 어떤 경향성을 가지고 있는지 선형 회귀로 예측해보려고 합니다.

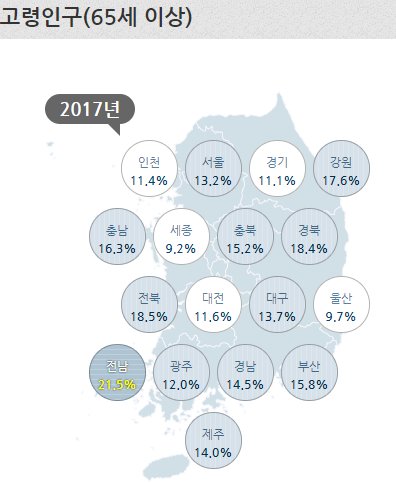
이 지표들을 시각화해보겠습니다.
import matplotlib.pyplot as plt
school_age_population = [16.4, 14.7, 17.2, 16.6, 17.1, 20.3, 17.2, 15.6, 17.4, 18.7, 16.9, 17.1, 15.8, 19.3, 16.6, 15.1, 17.9]
elderly_population = [11.4, 13.2, 11.1, 17.6, 16.3, 9.2, 15.2, 18.4, 18.5, 11.6, 13.7, 9.7, 21.5, 12.0, 14.5, 15.8, 14.0]
plt.plot(school_age_population, elderly_population, 'ko')
plt.xlabel('school_age_population(%)')
plt.ylabel('elderly_population(%)')
plt.show()
벌써 결과가 흥미롭네요. 이 그래프에서는 일반적인 경향을 깨뜨리는 극단치(outlier)는 보이지 않는 것 같습니다.
이제 이 데이터들로 선형 회귀를 해볼 차례인데요.
데이터의 경향성을 잘 나타내주는 직선과 데이터들의 차이를 잔차(residual)이라고 합니다.
이 잔차의 제곱을 최소화하는 알고리즘이 최소제곱법(Least Square Method)입니다.
post.naver.com/viewer/postView.nhn?volumeNo=29124872&memberNo=21815&vType=VERTICAL
보론: 최소제곱법(least squares method) 증명
[BY 안국이] 우리는 x 값이 주어졌을 때 y 값을 예측하고 싶습니다. 우리에게는 과거의 데이터 X와 Y가 ...
m.post.naver.com
이 블로그에 증명이 잘 정리되어 있으니 참고하시면 좋을 듯 합니다.
저희는 필요한 a와 b값만 가져오겠습니다.

각 데이터들의 값과 데이터의 평균들의 변수들로 이루어져 있네요.
이제 최소제곱법으로 a, b를 계산해 회귀선을 구해보겠습니다.
import matplotlib.pyplot as plt
import numpy as np
school_age_population = [16.4, 14.7, 17.2, 16.6, 17.1, 20.3, 17.2, 15.6, 17.4, 18.7, 16.9, 17.1, 15.8, 19.3, 16.6, 15.1, 17.9]
elderly_population = [11.4, 13.2, 11.1, 17.6, 16.3, 9.2, 15.2, 18.4, 18.5, 11.6, 13.7, 9.7, 21.5, 12.0, 14.5, 15.8, 14.0]
#평균 구하기
avg_school_age_population = sum(school_age_population) / len(school_age_population)
avg_elderly_population = sum(elderly_population) / len(elderly_population)
#a, b 초기화
a = 0
b = 0
#a 분자 구하기
a_up = 0
for y, x in list(zip(elderly_population, school_age_population)):
a_up += (y - avg_elderly_population) * (x - avg_school_age_population)
#a 분모 구하기
a_down = 0
for x in school_age_population:
a_down += ((x - avg_school_age_population)*(x - avg_school_age_population))
#a, b 값 구하기
a = a_up/a_down
b = avg_elderly_population - a * avg_school_age_population
#회귀선의 x, y 구하고 선 표현하기
line_x = np.arange(min(school_age_population), max(school_age_population), 0.1)
line_y = a * line_x + b
plt.plot(line_x, line_y, 'r-')
plt.plot(school_age_population, elderly_population, 'ko')
plt.xlabel('school_age_population(%)')
plt.ylabel('elderly_population(%)')
plt.show()

예측한대로 학령인구가 증가할수록 고령인구가 감소하는 경향을 가진 회귀선이 도출되었습니다.
'공부 > tensorflow' 카테고리의 다른 글
| [tensorflow 12] 다항회귀 (0) | 2021.04.21 |
|---|---|
| [tensorflow 11] 선형회귀02 (0) | 2021.04.20 |
| [tensorflow 09] XOR 네트워크 시각화 (0) | 2021.04.13 |
| [tensorflow 08] matplotlib.pyplot 시각화 (0) | 2021.04.12 |
| [tensorflow 07] XOR 연산 뉴런 (0) | 2021.04.09 |




